Resting state FSLnets practical

FSLNets is a toolbox for carrying out basic network modelling from FMRI timeseries data. It is a collection of Python functions that run a connectivity analysis between sets of timeseries.

Estimating network matrices and performing statistical analyses on these requires the following steps:

1. Extracting subject-specific timeseries relating to a given set of spatial maps of nodes. For example, using dual regression stage 1 outputs
2. Looking for group-level noise components that you want to remove
3. Calculating correlations (full or partial) between all pairs of timeseries to build the network matrix (netmat) for each subject
4. Looking at the group-average network matrix and how nodes cluster together into a hierarchy
5. Performing group-level statistical analysis

Contents:

Before running FSLnets

Defining nodes and edges to run network modelling analysis

Networks estimation

Estimating network matrices from dual regression outputs

Group-average netmat summaries

Calculating group-average netmats

Cross-subject comparison with netmats

Comparing individual edge strengths between subject groups

(Optional) Multivariate cross-subject analysis

Multivariate comparison of whole netmats across subject groups

In the next sections we will go through an example of how to perform network modelling using resting-state data (i.e. the output from melodic followed by stage 1 of dual regression). However, with FSLNets you can analyse any set of timeseries!

Before running FSLnets

Before you run FSLnets, you need to prepare several things:

• Define 'nodes'

The nodes are the spatial maps that define the regions included in our network modelling. Nodes can be defined in a number of ways, but for this practical we have already generated the nodes for you using the following group ICA command to extract 100 components (please do not run this again):

melodic -i input_files.txt -o groupICA100 \
  --tr=0.72 --nobet -a concat \
  --bgimage=$FSLDIR/data/standard/MNI152_T1_2mm_brain.nii.gz \
  -m $FSLDIR/data/standard/MNI152_T1_2mm_brain_mask.nii.gz \
  --report --Oall -d 100

Nodes could also be defined using anatomical or functional atlases, although anatomical atlases may not provide good functional parcellations as the structural boundaries are not always a good estimate of functional boundaries.
• Extract timeseries from nodes

To look at the temporal relationship between our nodes, we must first extract the timeseries from each node. Again, the timeseries extraction can be done in a number of ways. For this practical, we have already extracted the timeseries from the 100 nodes by running dual regression with the command below, and using the stage 1 output.

dual_regression groupICA100/melodic_IC 1 -1 0 groupICA100.dr $(cat input_files.txt)
  

• Create images of nodes

For visualisation purposes, FSLnets requires a PNG image of each node. We have created these for you (located in ~/fsl_course_data/rest/Nets/group100.sum) using the following command:

If you are using Group ICA to define your nodes, FSLNets can generate the node thumbnails for you - have a look at the nets.load help documentation for more details.




In fact, if you are planning to use dual regression to extract the per-subject node time series, you can use the nets.load_from_images function to perform the first stage of dual regression for you.

slices_summary groupICA100/melodic_IC 4 \
  $FSLDIR/data/standard/MNI152_T1_2mm   \
  groupICA100.sum -1

This command takes the 4D image containing the group ICA components (groupICA100/melodic_IC), sets a minimum threshold of 4, specifies the MNI152_T1_2mm as the background image, and creates the output directory groupICA100.sum, which contains the png images of each node. The -1 flag specifies that single-slice summaries should be generated instead of 3-slice summaries.

Getting started

To start this FSLNets network modelling practical, open a terminal and cd to the working directory of this practical, then start a Python session by running fslipython:

cd ~/fsl_course_data/rest/Nets
fslipython

The remainder of this practical will take place within this Python session. Let's start by importing the fsl.nets package, and configuring matplotlib for plotting:

%matplotlib
from fsl import nets

Networks estimation

Now we are ready to start setting up some important parts for our network modelling analysis. To load in all subjects' timeseries data files from the dual-regression output directory, run:

ts = nets.load('groupICA100.dr',
               0.72,
               varnorm=0,
               thumbnaildir='groupICA100.sum');

Explore the ts object - type in ts., and then press the TAB key to bring up a list of the fields contained in the ts object. You can bring up the help documentation for any fields by typing ts.‹fieldname›? and pushing enter. For example, type ts.ts? and push enter - this field contains the stage 1 dual regression timeseries from all subjects. Try to figure out what information the other fields in the ts object contain.

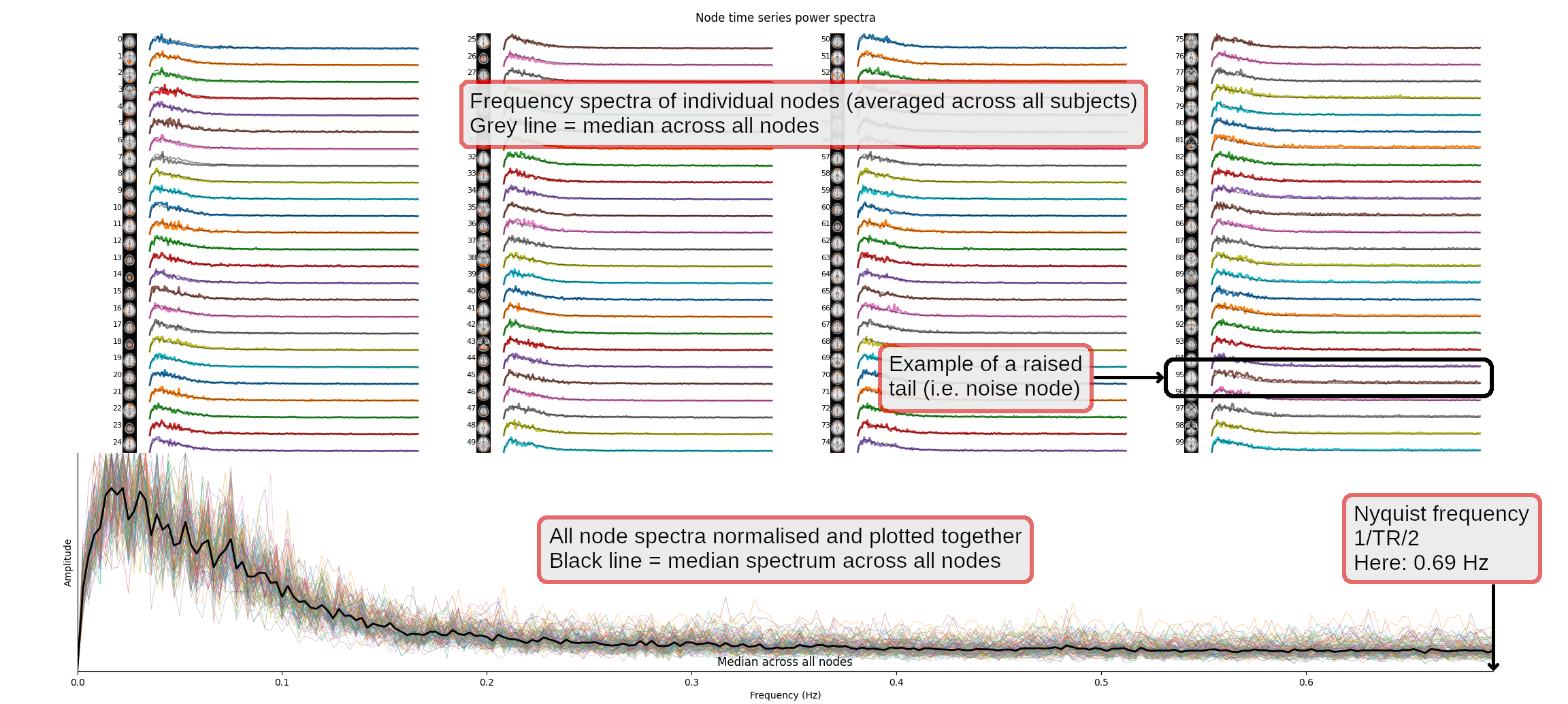
We will now have a quick look at the temporal spectra of the resting state networks (RSNs), as a quick check that these look reasonable. Running the following command will open a figure in which the top part of the plot shows one spectrum per group-ICA component, each averaged across all subjects. The bottom part shows the same thing, but with all spectra overlapping, and the median power spectra across all runs as a thick black line.

nets.plot_spectra(ts);

Cleaning components

There is the option to remove components' (nodes') timeseries that correspond to artefacts rather than plausible nodes. Similarly to the last practical, you need to decide this by looking at the spatial maps, timeseries, and frequency spectra. To save time, we have listed the good components for you. Run the following commands to list the good components and apply the cleanup (remember, you can type nets.clean? to bring up the documentation for the nets.clean function, or any other FSLNets function):

goodnodes = [0,  1,  2,  4,  5,  6,  7,  8,  10, 11,
             12, 16, 17, 18, 19, 20, 21, 22, 24, 25,
             26, 27, 28, 29, 30, 31, 32, 33, 34, 35,
             36, 37, 39, 41, 42, 46, 47, 48, 49, 51,
             52, 54, 55, 56, 57, 58, 60, 61, 63, 64,
             65, 69, 70, 71, 72, 73, 76, 79, 80, 85,
             86, 92, 96]

nets.clean(ts, goodnodes, True)

Calculating netmats for each subject

Now you are ready to compute a network matrix for each subject, which is in general a matrix of correlation strengths (correlation coefficients). We will compute two different versions of these netmats for each subject: a simple full correlation ('corr'), and a partial correlation that has been regularised in order to potentially improve the mathematical robustness of the estimation ('ridgep'). The partial correlation matrix should do a better job of only estimating the direct network connections than the full correlation does.

Note:

F

P

Fnetmats = nets.netmats(ts, 'corr',   True)
Pnetmats = nets.netmats(ts, 'ridgep', True, 0.1)

The full and partial netmats are now calculated for all subjects. Now run this command to look at the size of the Fnetmats variable:

Fnetmats.shape

Can you figure out how the netmats of all subjects are saved in this? Answer.

In the next section, you are going to compute the group average and take a look at the average network matrix.

Group-average netmat summaries

We have computed the full and partial network matrices for each individual subject. The next step is to perform a simple group-level analysis to look at the mean network matrix across all subjects. This can be done using the command below, which saves out both the simple average of netmats across all subjects (Mnet) and the results of a simple one-group t-test (against zero) across subjects as Z values (Znet).

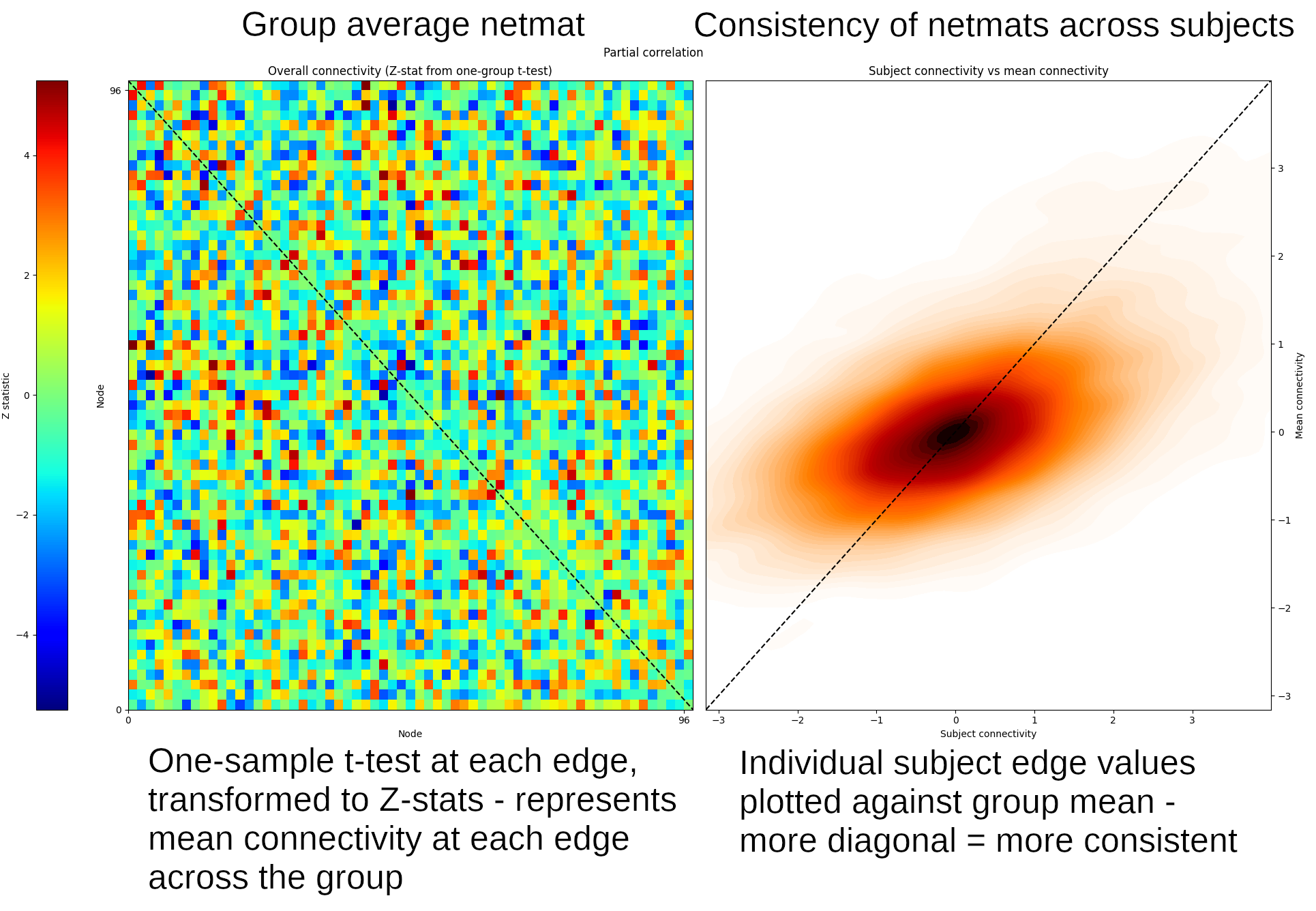
Znet_F, Mnet_F = nets.groupmean(ts, Fnetmats, False)
Znet_P, Mnet_P = nets.groupmean(ts, Pnetmats, True, 'Partial correlation')

If you see the message "invalid value encountered in true_divide", don't be alarmed. This is ok for this example. The plots that we create with the above commands may also take some time to generate, so please be patient.

The third input to this command indicates whether or not to display a summary figure. This is set to True for the second command run on the partial netmats, so the summary figure for this will show up (the fourth argument, "Partial correlation" allows you to set the plot title). On the left, this figure shows the results from the group t-test, and on the right is a consistency scatter plot showing how similar the results from each subject are to the group (i.e. the more this looks like a diagonal line, the more consistent the relevant netmat is across subjects).

The value of Mnet_P in row 3, column 27 is ~6.6 (you can check this by typing Mnet_P[2, 26] into Python and hitting enter - Python starts counting from 0, so row 3 is referenced using the index 2, and column 27 referenced using index 26).

Note that the node numbers used above (2 and 26) are referring to the locations, (a.k.a. indexes) of nodes in the netmats after removal of noise nodes via nets.clean. This may not be the same as the original node indexes before nets.clean. You can find out the original node index via ts.nodes - for example, try running ts.nodes[2] and ts.nodes[26] - do you understand the meaning of the results? Click here for the answer.

Group average network hierarchy

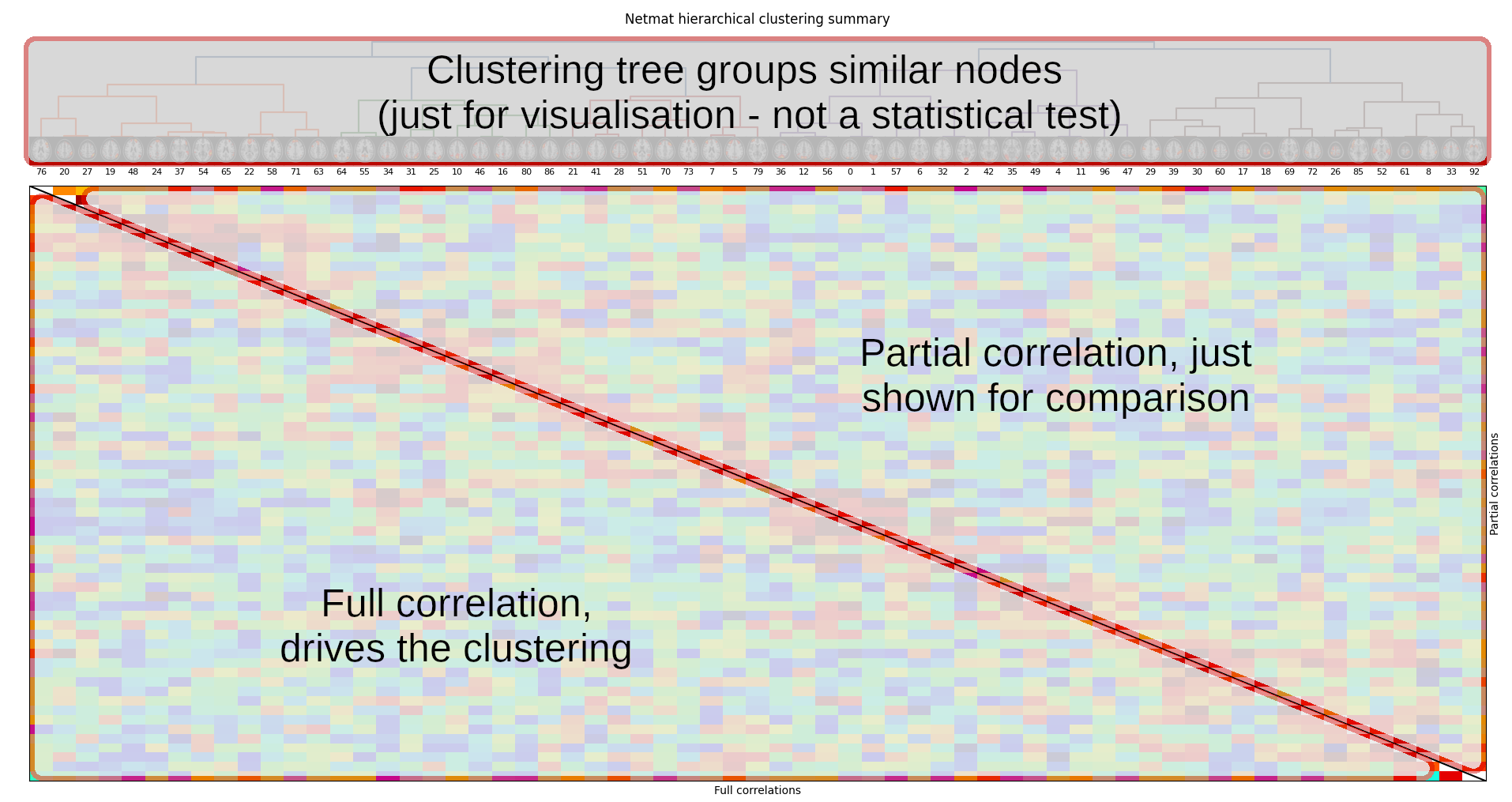
The next thing we can look at is how nodes cluster together to form larger resting state networks. For this we run a clustering method that groups nodes together based on their covariance structure. To view this network hierarchy, run:

nets.plot_hierarchy(ts, Znet_F, Znet_P, 'Full correlations', 'Partial correlations')

If you look closely, you might be able to see a set of nodes which have been grouped together, and which resemble a large-scale resting state network called the default mode network (that you may have heard about).

It is possible to visualise this hierarchical arrangement in a different way, using the nets.netweb function. Run the following code - it will open a new tab in your web browser:

nets.web(ts, (Znet_F, Znet_P), ('Full correlation', 'Partial correlation'))

This page displays the same clustered node hierarchy (known as a dendrogram) arranged in a circle, with the top of the hierarchy (the root) in the centre, and the nodes (the leaves) around the perimeter. You can click on a node to highlight the connectivity from that node to its most strongly connected neighbours.

Cross-subject comparison with netmats

We are now able to test whether the netmats differ significantly between healthy controls and patients with a tumor using a two-sample t-test. This is a 'univariate' test, as we will test each network matrix edge separately for a group-difference, and then we will estimate p-values for these tests, correcting for multiple comparisons across all tests. By analogy to high-level task-fMRI analyses: you can think of each subject's netmat as being an NxN image of voxels, and the univariate testing as modelling each voxel (in isolation from each other) across subjects.

We have already created the design files for you to run the two-sample t-test. If you want to look at the design, open the GLM GUI (in a new terminal window) and load the ~/fsl_course_data/rest/Nets/design/unpaired_ttest_1con.fsf file (ignore the error message, go to the 'stats' tab and click 'full model setup' to be able to see the design).

p_corr,p_uncorr = nets.glm(ts, Pnetmats, 'design/unpaired_ttest_1con.mat', 'design/unpaired_ttest_1con.con');

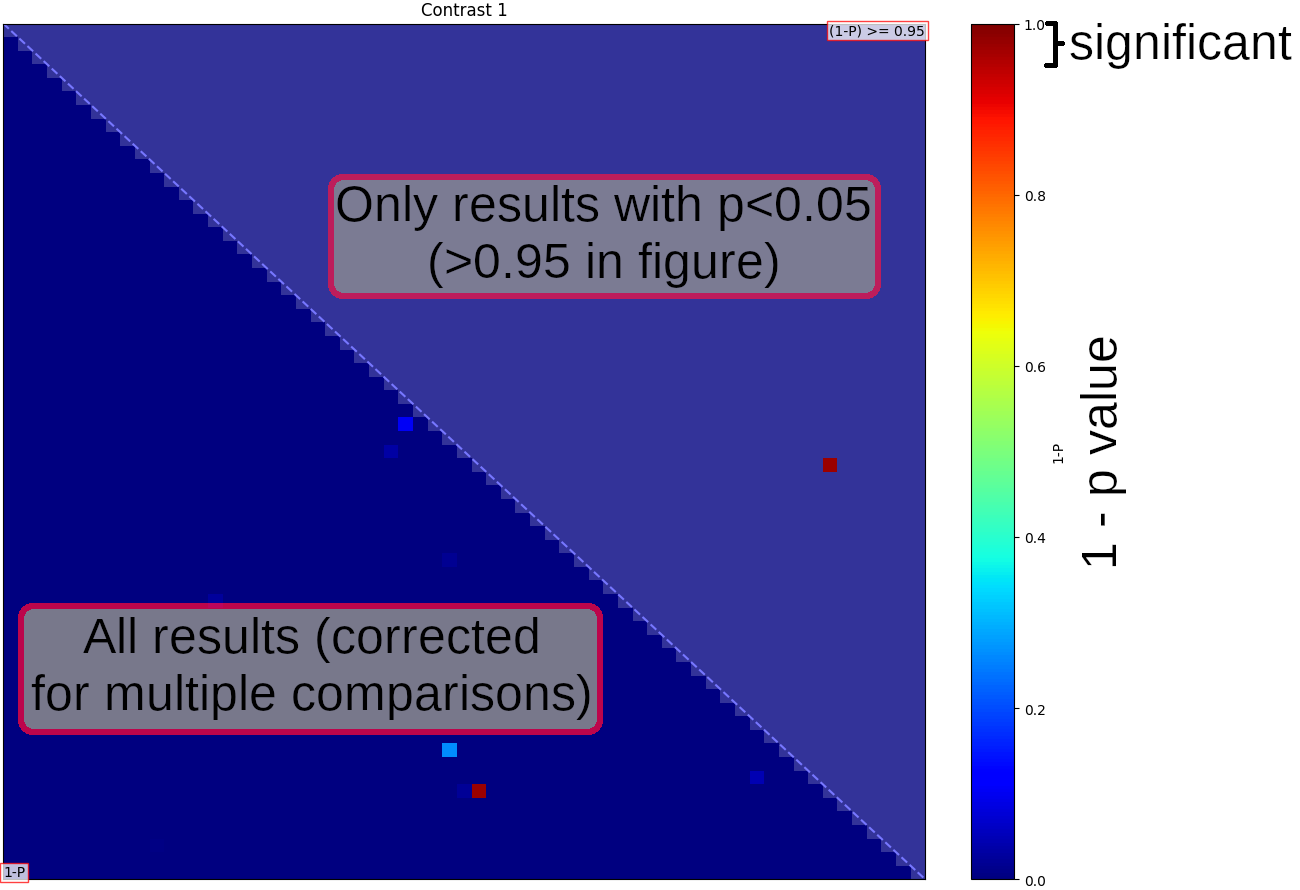
Once randomise has finished, you will see a figure showing "netmats" containing corrected p-values. The results above the diagonal show edges where the two-group t-test is significant, at corrected-p<0.05.

Displaying significant group differences

We will now run a command that shows which nodes and edges were linked to the strongest differences between the groups:

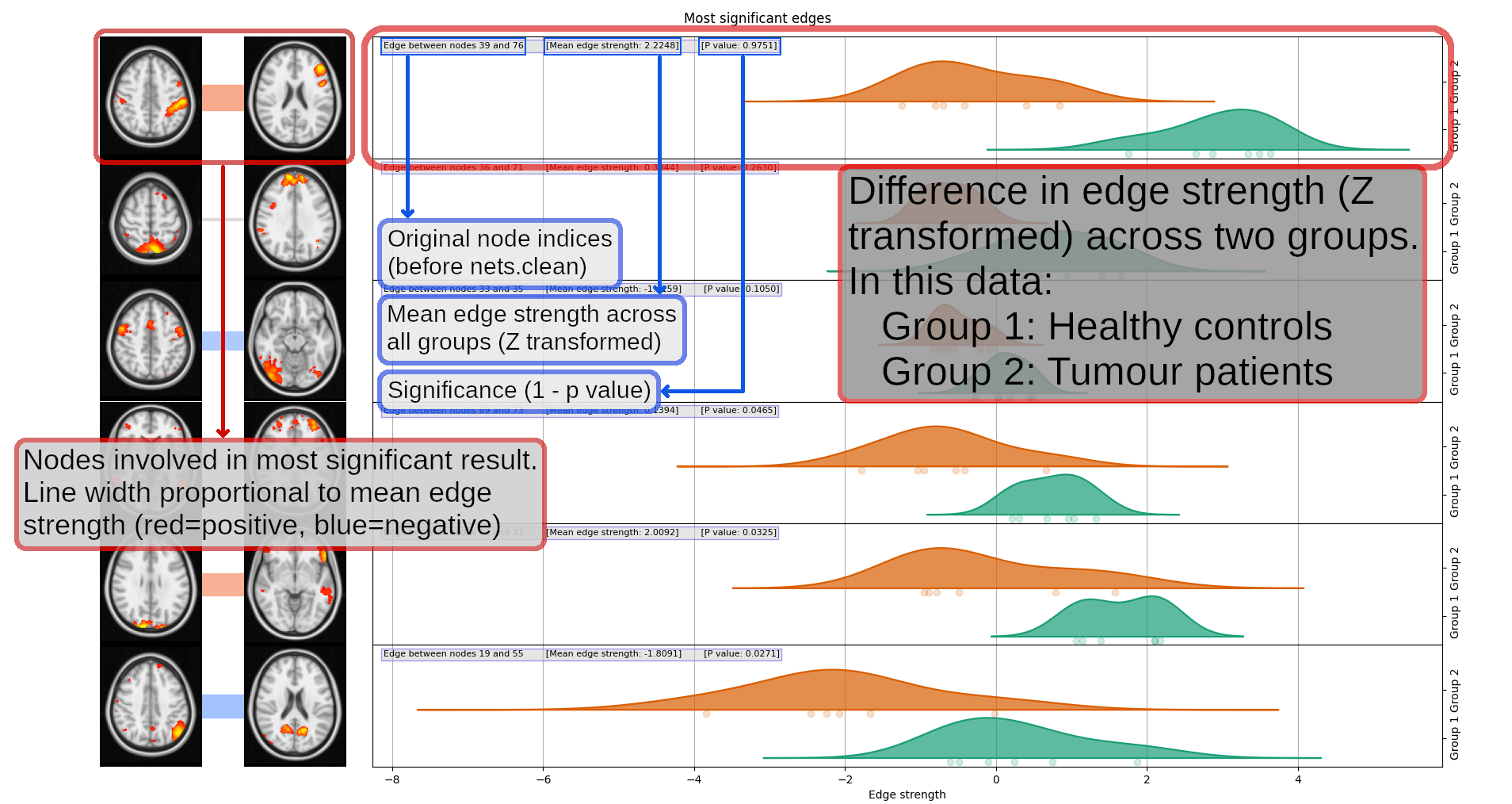
nets.boxplots(ts, Pnetmats, Znet_P, p_corr[0], groups=(6, 6))

Each pair of thumbnails corresponds to one position in the NxN network matrix and the node numbers are listed in the text captions. The coloured bar joining each pair of nodes tells you what the overall group-average connection strength is: thicker means a stronger connection; red means it's positive, and blue means that the connection is "negative" (meaning that the two nodes tend to anti-correlate on average). The "P value" numbers tell you the 1-p-values - so the higher these are, the more significantly different this edge strength is between the two groups. Anything less than 0.95 is not significant, after correcting for multiple comparisons.

The plots on the right show how the partial correlation differs between the patients and the controls for each of the edges with the strongest group difference. The plots summarise the distributions of the correlation values (connection strengths) in the two groups - Group 1 being healthy controls in this data, and Group 2 being tumour patients - for each node-pair.

If you are finishing the practical here and not doing the optional section below, type exit in the terminal to exit Python.

(Optional) Multivariate cross-subject analysis

Finally, we will now carry out multivariate cross-subject analysis - meaning that, instead of considering each netmat edge in isolation (like we did above) we will consider the whole netmat in one analysis.

For example, we can attempt to classify subjects into patients or controls using machine learning methods, such as support vector machines (SVM) or linear discriminant analysis (LDA). Such methods look at the overall pattern of values in the netmat, and try to learn how the overall pattern changes between the two groups.

The following command feeds the regularised partial correlation netmats from both groups into LDA. It uses a method known as leave-one-out cross-validation to train and test a classifier, and reports in what percentage of tests it was successful at discriminating between patients and controls:

nets.classify(Pnetmats, (6, 6))

This function uses the scikit-learn library to perform classification. You can use any other classifier available in scikit-learn by passing a third argument to nets.classify. For example, to use a random forest classifier:

from sklearn.ensemble import RandomForestClassifier
nets.classify(Pnetmats, (6, 6), RandomForestClassifier())

One "downside" of such multivariate testing is that you can no longer make strong statistical claims about individual edges in the network - the whole pattern of edges has been used, so we don't know which individual edges are significantly different in the two groups.

Type exit in the terminal to exit Python.

The End.